> >
RC Corbel Design
| Download Sample Report |
The scope of this calculation module is to design a concrete corbel intended to carry high vertical and horizontal load transferred from the adjacent beam without monolithic connection. The program calculates the area of main and shear reinforcement required for the section. When the depth of the corbel is specified as ‘uniform’, it is treated as ‘nib’ and the design is carried out accordingly.
Strut and Tie Anology
ECPLUS DESIGN adopts strut and tie analogy to design the corbel as follows:
British Standard
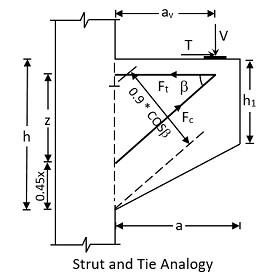
The tension in the strut is calculated as,
Ft = Fc * cos(β) + T = (V * av) / z + T
The compression in the strut is calculated as,
Fc = (0.67 * fcu) / (1.5) * b * 0.9 * x * cos(β) = 0.402 * fcu * b * x * cos(β)
Equating to the vertical load,
V = Fc * sin(β)
and the lever arm distance,
z = d – 0.45 * x
The equations are solved for x by iterative method.
European Standard
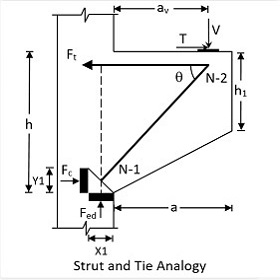
The horizontal concrete compression force at node 1 is calculated as,
Fc = γ * b * σrdmax
Strut force is calculated as,
Fst = (Fc * cos(θ)) + (V * sin(θ))
Concrete strut stress,
σst = Fst / (a1 * b)
Where a1 is width of concrete strut and b is width of the corbel
Maximum design shear resistance is calculated by the following formula,
Vrdmax = (αcw * b * z * v1 * fcd) / (cot(θ) + tan(θ))
The area of reinforcement is calculated by total tension by reinforcement grade.
American Standard
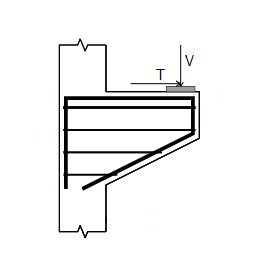
Nominal vertical load and vertical load capacity is calculated as,
Vn = V / (0.75)
Vncap = min(0.2 * f'c * b * d, (480 + 0.08 * f'c) * b * d, 1600 * b * d)
Calculation of moment is carried out as,
Mu = V * av + Th * (h - d)
Area of shear friction reinforcement is calculated as,
Avf = Vn /(1.4 * fy)
Af = Mn / (fy * Φ * 0.85 * d)
Then, area of tension reinforcement is calculated as,
Asreq = max(0.67 * Avf + An, Af + An, Amin)
Area of horizontal reinforcement required is calculated by following formula,
Ahreq = max(Avf / 3, Af / 2, Ahmin)
Features
- The program checks for the adequacy of the tension reinforcement for given loads.
- The calculation includes bearing stress, bond stress and shear capacity of the section.
- The member is designed as a nib, when the overall depth and free end depth is defined as uniform.
- Crack width is calculated if required by the user.
Design Considerations
- If distance from load to column face is less than half of the overall depth of corbel, then closed horizontal links should be provided in addition to the main tension reinforcement.
- If distance from load to column face is greater than half of the overall depth of corbel, then closed vertical links should be provided in addition to the main reinforcement.
- The main reinforcement should be fully anchored into the column and the other end of these bars should be welded to an anchorage device.
- The shear link provided must be closed type links.
- Distribution depth for shear reinforcement is considered as two third of the effective depth of the section.
- For crack width calculation, moment at serviceability state shall be specified.
National Standards Available
British Standard
Europe Standard
- National Annex of several countries such as Europe (Recommended), UK, Finland, Ireland, Malaysia, Norway, Singapore, Sweden are considered.
- Additionally, an option is provided to define the coefficients directly by the user.
American Standard
- The calculation allows the user to design the section both in imperial and metric units.
References
- Reinforced Concrete - Analysis and Design by S.S. Ray published by Blackwell Science.
- BS 8110-1:1997 - Structural use of concrete - Part 1: Code of practice for design and construction.
- EN1992-1-1:2004 - Design of concrete structures - Part 1-1: General rules and rules for buildings.
- ACI 318-14 - Building Code Requirements for Structural Concrete.
- ACI-224R-01 - Control of Cracking in Concrete Structures.
Revision
- Ver 1.0 - Original version
| Download Sample Report |